Unit 8 Maths for Construction, Higher National Certificate Construction and the Built Environment

Assignment - Assisting with Construction Mathematical problems

Learning Outcome 1: Use analytical and computational methods to solve construction related problems

Learning Outcome 2: Investigate applications of statistical techniques to interpret, organise and present data by using appropriate computer software packages

Learning Outcome 3: Illustrate the wide-ranging uses of calculus within different construction disciplines by solving problems of differential and integral calculus

Learning Outcome 4: Use mathematical methods to solve vector analysis, arithmetic progression and dimensional analysis examples.

Examination 1

You are required to evaluate the construction problems below and justify, were applicable, the techniques adopted to solve such problems.

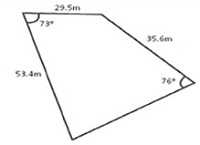
1A. You have surveyed one of the building sites which your company is to develop. It is in the form of a quadrilateral as shown in the figure below. You are asked to determine:
i. the length of the perimeter of the site.
ii. the total area of the site to be developed.

1B. A simply supported beam of S355 strength steel is required to support a load (W) of 333 kN. The span of the beam (L) is 5.5m. You are asked to:

i. Calculate the deflection of the beam in (mm). The deflection formula can be expressed by:

1C. Solve the following simultaneous equations:

2x + y = 5

and

x² - y² = 3

1D. A formula for the velocity (v) of waves in shallow water is:

v² = 0.55Ltanh(6.3d/L)

Where: d is the depth 

L is the wavelength

i. If d = 9.0 and L = 92, calculate the value of v.

1E. The mass, in grams, of a ball bearing varies directly with the cube of the radius, measured in millimetres. A ball bearing of radius 4 mm has a mass of 115.2g. Calculate the following:

i. A ball bearing has a radius of 6 mm. What is its mass?

ii. A ball bearing has a mass of 48.6kg. What is its radius?

1F. Undertake the following:

i. Evaluate the following matrices:

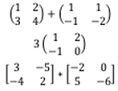
ii. Transpose the matrix:

iii. Find the inverse of the matrix:

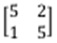
1G. Concrete strength is usually related to its strength at 28 days based on the load that a standard cube of concrete can sustain when tested in compression in a compression testing rig. The data below contains the results for a series of 40 concrete strength tests undertaken on a construction project currently being developed by your company.

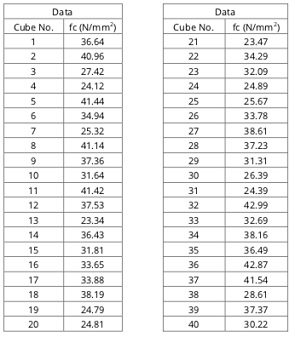
You are required to summarise this data and calculate the following:

i. the mean strength

ii. the median strength

iii. the standard deviation for the results

iv. the percentage of blocks which fall between +/- one standard deviation
(a) Determine the actual number
(b) Determine the number if a normal distribution is assumed
(c) Comment on any similarity or difference between answer (a) and (b)

v. estimate the probability that the strength of a given concrete cube will exceed 37 N/mm2 (Assume Normal distribution with mean and standard deviation determined earlier)

vi. apply binomial distribution methods to determine the probability of testing a cube which will exceed 37 N/mm2 within the next 5 tests. (Use probability from (v) for binomial calculation)

1H. You have been asked to interpret data from a hypothesis test. A test was conducted for two proportions to evaluate if they are the same. Within the laboratory, an R&D project was developed to assess a newly designed concrete in two batches, sample A and sample B. A batch from sample A evaluated that 51 designs from a sample of 190 models was successful. However, a batch from sample B determined 323 simulated models succeeded in a sample of 601.

The null hypothesis (H0) for the test is that the proportions are the same, and the alternate hypothesis (H1), is that the proportions are not the same.

Use a 5% alpha (confidence) level to determine if the two batches are comparable? Illustrate all steps of your method before assessing if the data is comparable, in terms of accepting or rejecting the ‘null hypothesis'.

Examination 2

You are required to analyse differential calculus techniques.

2A. Differentiate the following:

i. 5x⁴

ii. e^{sin 2x}

iii. l n cos (3x)

iv. (3x² - 2x + 7)²

2B. Integrate the following definite and indefinite integrals:

(i) ∫(3 x² +2x +5)dx
(ii)∫(2-7x)⁵ dx
(iii)∫(sec² x)/tanx dx
(iv) ∫x² e^3x dx
(v)∫1/√(4-x² ) dx Hint use substitution x=2sinθ?

2C. Undertake the following:

i. Sketch the functions y = x² and y = 8 - x² on an x-y system of axes and using integral calculus determine the area enclosed by them.
ii. The area from part A is rotated 360o about the x-axis. Using integral calculus determine the volume produced

2D. A continuous steel beam in a framed structure is to be checked. The bending moment M due to external forces acting on the beam is given by the equation below, where L is the horizontal distance along the beam's span.

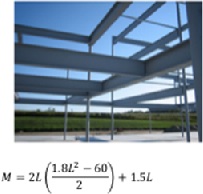
Using differential calculus, determine the following:
i. the distance at which the beam experiences its maximum and minimum bending stress
ii. the value of L when the bending stress is zero.
iii. What are the steps in the method for finding the maximum or minimum value of the function?
iv. Explain why there might be one point which is a zero of the derivative but not a local maxima or minima. Give examples and support your answer using sketches or diagrams.

Examination 3

You are required to evaluate the effectiveness and relevance, to the solving of construction problems, of the mathematical techniques of vector analysis, arithmetic progression and dimensional analysis

3A. A steel frame tower is held in place by three cables. If the force of each cable FDA, FDB and FDC acting on the tower is shown, determine the magnitude and coordinate direction angles of the resultant force FR.

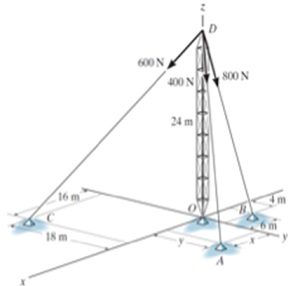
i. Use a cartesian vector notation (i, j, k). Take x = 20 m, y = 15 m.

3B. A pipeline is to be fitted under a road and can be represented on 3D Cartesian axes as below, with the x-axis pointing East, the y-axis North, and the z-axis vertical. The pipeline is to consist of a straight section AB directly under the road, and another straight section BC connected to the first. All lengths are in metres.

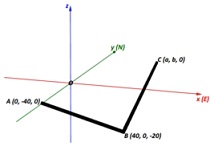
i. Calculate the distance AB
ii. The section BC is to be drilled in the direction of the vector 3i +4j + k
Find the angle between the sections AB & BC

3C. The company needs to bore a hole 120m deep.

i. Estimate, using arithmetic progression, the cost of boring, if the cost is £70 for drilling the first metre with an increase in cost of £3 per metre for each succeeding metre.

3D. A brick supplier produced product charges by the following method.

Quantity Price:

1 pallet of 500 bricks £300

2nd pallet of 500 bricks £295

3rd pallet of 500 bricks £290 and so on with a maximum order of 5000 bricks.

i. Using arithmetic progression determine how much an order of 5000 bricks
would cost.

3E. The energy head loss K in a flow system is to be determined using the Bernoulli's equation shown below:

p/ρg + v²/2g + h = K

Where: v =  3.1 m/s

p = 200 kN/m²

ρ = 1000 kg/m³

g = 9.81 m/s²

h = 6m

i. Determine the total head loss.

ii. Using dimensional analysis, establish the SI unit for the final value.